
DIAGRAMA DE CAJA:Un diagrama de caja es un gráfico, basado en cuartiles, mediante el cual se visualiza un conjunto de datos. Está compuesto por un rectángulo, la caja, y dos brazos, los bigotes.
Es un gráfico que se suministra información sobre los valores mínimo y máximo, los cuartIles Q1, Q2 o mediana y Q3, y sobre la existencia de valores atípicos y simetría de la distribución:
Es un gráfico que se suministra información sobre los valores mínimo y máximo, los cuartIles Q1, Q2 o mediana y Q3, y sobre la existencia de valores atípicos y simetría de la distribución:
COMO SE CONSTRUYE UN DIAGRAMA DE CAJA O BLOX--PLOT:
Ordenar los datos y obtener el valor mínimo, el máximo, los cuartiles Q1, Q2 y Q3 y el rango intercuartil (IQR)
En el ejemplo: Valor 7: es el Q1 (25% de los datos) Valor 8.5: es el Q2 o mediana (el 50% de los datos) Valor 9: es el Q3 (75% de los datos) Rango intercuartil IQR (Q3-Q1)=2
Dibujar un rectángulo con Q1 y Q3 como extremos e indicar la posición de la mediana (Q2) mediante una línea.
Para dibujar los bigotes, las líneas que se extienden desde la caja, hay que calcular los límites superior e inferior, Li y Ls, que identifiquen a los valores atípicos.
Para ello se calcula cuando se consideran atípicos los valores. Son aquellos inferiores a Q1-1.5*IQR o superiores a Q3+1.5*IQR. En el ejemplo: inferior: 7-1.5*2=4 superior: 9+1.5*2=12 Ahora se buscan los últimos valores que NO son atípicos, que serán los extremos de los bigotes. En el ejemplo: 5 y 10
Marcar como atípicos todos los datos que están fuera del intervalo (Li, Ls).
En el ejemplo: 0.5 y 3.5 Pero además se pueden considerar valores extremadamente atípicos a los que exceden Q1-3*IQR o Q3+3*IQR. De tal modo que, en el ejemplo: inferior: 7-3*2=1 superior: 9+3*2=15 El valor 0.5 seria atípico extremo y 3.5 sería atípico.
Proporcionan una visión general de la simetría de la distribución de los datos, si la media no está en el centro del rectángulo, la distribución no es simétrica.
Son útiles para ver la presencia de valores atípicos.
COMENTARIO: EL DIAGRAMA DE CAJA O DE BLOX--PLOT ESTE No es más que un grafico a traves del cual podemos representar los cuartiles 1,2,3 , la mediana asi
mismo sirve para para establecer datos a típicos los cuales los podemos encontrar o ubicar en el diagrma de cajas en el tambien neceitamos pasos y formulas a aplicar para asi determinar si las barreras ( interior superio, interior inferior, exterir inferior, exterior superior los establecemos alli o se encuentran fuera y determinamos los datos atípicos
1. barrera interior y barrera exterior: cuando los datos se encuentran alli los datos son a tipicos
2. si se encuentran datos despues de la barrera exterior se les llama datos a atipicos externos.
para determinar el rango intercuartilico necesitamos: restar Q1-Q3. Lo obtendremos para asi calcular las barreras.
la estadistica es base primordial en cual quier ambito a calcular..........
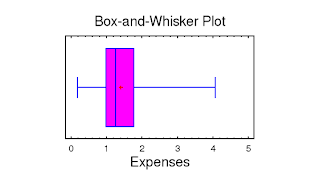

el diagrama de caja es una grafico a traves del cual podemos representar los datos cuartilicos .
ResponderEliminarel diagrma de caja es un grafico a traves del cual representamos datos asi como los cuartiles (Q1, Q2, Q3 ) pero asi mismo la medina por si lo encontramos antes o después del cuartil Q2(MEDIA) CALCULANDO tambén los bigotes de la caja a medida de la escla establecida del dato menor al mayor.
ResponderEliminareste blogg me parecio muy bien porque esta al dia de los temas visto en clase durante estos dias.........10
ResponderEliminarmuchas gracias!!
ResponderEliminarEl diagrama de caja y bigote es una herramienta para analisis visual de los datos, es decir una herramienta para dejar que los datos hablen. Es tambien llamado analisis de los cinco puntos
ResponderEliminar