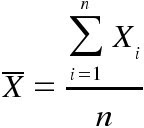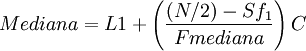PECENTILES MEDIDAS DE POSICION
PECENTILES MEDIDAS DE POSICIONmartes, 24 de marzo de 2009
DIAGRAMA DE TALLOS Y HOJAS


En muestreo se entiende por población a la totalidad del universo que interesa considerar, y que es necesario que esté bien definido para que se sepa en todo momento que elementos lo componen.
No obstante, cuando se realiza un trabajo puntual, conviene distinguir entre población teórica: conjunto de elementos a los cuales se quieren extrapolar los resultados, y población estudiada: conjunto de elementos accesibles en nuestro estudio.
Censo: En ocasiones resulta posible estudiar cada uno de los elementos que componen la población, realizándose lo que se denomina un censo, es decir, el estudio de todos los elementos que componen la población.
La realización de un censo no siempre es posible, por diferentes motivos: a) economía: el estudio de todos los elementos que componen una población, sobre todo si esta es grande, suele ser un problema costoso en tiempo, dinero, etc.; b) que las pruebas a las que hay que someter a los sujetos sean destructivas; c) que la población sea infinita o tan grande que exceda las posibilidades del investigador.
Si la numeración de elementos, se realiza sobre la población accesible o estudiada, y no sobre la población teórica, entonces el proceso recibe el nombre de marco o espacio muestral.
Concepto de muestreo :
El muestreo es una herramienta de la investigación científica. Su función básica es determinar que parte de una realidad en estudio (población o universo) debe examinarse con la finalidad de hacer inferencias sobre dicha población. El error que se comete debido a hecho de que se obtienen conclusiones sobre cierta realidad a partir de la observación de sólo una parte de ella, se denomina error de muestreo. Obtener una muestra adecuada significa lograr una versión simplificada de la población, que reproduzca de algún modo sus rasgos básicos.
Muestra: En todas las ocasiones en que no es posible o conveniente realizar un censo, lo que hacemos es trabajar con una muestra, entendiendo por tal una parte representativa de la población. Para que una muestra sea representativa, y por lo tanto útil, debe de reflejar las similitudes y diferencias encontradas en la población, ejemplificar las características de la misma.
Cuando decimos que una muestra es representativa indicamos que reúne aproximadamente las características de la población que son importantes para la investigación.
a. Población Los estadísticos usan la palabra población para referirse no sólo a personas si no a todos los elementos que han sido escogidos para su estudio. b. Muestra Los estadísticos emplean la palabra muestra para describir una porción escogida de la población. Matemáticamente, podemos describir muestras y poblaciones al emplear mediciones como la Media, Mediana, la moda, la desviación estándar. Cuando éstos términos describen una muestra se denominan estadísticas.
- 1 -
Una estadística es una característica de una muestra, los estadísticos emplean letras latinas minúsculas para denotar estadísticas y muestras. 2. - Tipos de muestreo Los autores proponen diferentes criterios de clasificación de los diferentes tipos de muestreo, aunque en general pueden dividirse en dos grandes grupos: métodos de muestreo probabilísticos y métodos de muestreo no probabilísticos.
Terminología
Población objeto: conjunto de individuos de los que se quiere obtener una información.
Unidades de muestreo: número de elementos de la población, no solapados, que se van a estudiar. Todo miembro de la población pertenecerá a una y sólo una unidad de muestreo.
Unidades de análisis: objeto o individuo del que hay que obtener la información.
Marco muestral: lista de unidades o elementos de muestreo.
Muestra: conjunto de unidades o elementos de análisis sacados del marco.
Muestreo probabilístico
Los métodos de muestreo probabilísticos son aquellos que se basan en el principio de equiprobabilidad. Es decir, aquellos en los que todos los individuos tienen la misma probabilidad de ser elegidos para formar parte de una muestra y, consiguientemente, todas las posibles muestras de tamaño n tienen la misma probabilidad de ser elegidas. Sólo estos métodos de muestreo probabilísticos nos aseguran la representatividad de la muestra extraída y son, por tanto, los más recomendables. Dentro de los métodos de muestreo probabilísticos encontramos los siguientes tipos:
El método otorga una probabilidad conocida de integrar la muestra a cada elemento de la población, y dicha probabilidad no es nula para ningún elemento.
Los métodos de muestreo no probabilisticos no garantizan la representatividad de la muestra y por lo tanto no permiten realizar estimaciones inferenciales sobre la población.
(En algunas circunstancias los métodos estadísticos y epidemiológicos permiten resolver los problemas de representatividad aun en situaciones de muestreo no probabilistico, por ejemplo los estudios de caso-control, donde los casos no son seleccionados aleatoriamente de la población.)
Entre los métodos de muestreo probabilísticos más utilizados en investigación encontramos:
Muestreo aleatorio simple
Muestreo estratificado
Muestreo sistemático
Muestreo polietápico o por conglomerados
- 2 -
Muestreo aleatorio simple:
El procedimiento empleado es el siguiente: 1) se asigna un número a cada individuo de la población y 2) a través de algún medio mecánico (bolas dentro de una bolsa, tablas de números aleatorios, números aleatorios generados con una calculadora u ordenador, etc.) se eligen tantos sujetos como sea necesario para completar el tamaño de muestra requerido.
Este procedimiento, atractivo por su simpleza, tiene poca o nula utilidad práctica cuando la población que estamos manejando es muy grande.
Muestreo aleatorio sistemático:
Este procedimiento exige, como el anterior, numerar todos los elementos de la población, pero en lugar de extraer n números aleatorios sólo se extrae uno. Se parte de ese número aleatorio i, que es un número elegido al azar, y los elementos que integran la muestra son los que ocupa los lugares i, i+k, i+2k, i+3k,...,i+(n-1)k, es decir se toman los individuos de k en k, siendo k el resultado de dividir el tamaño de la población entre el tamaño de la muestra: k= N/n. El número i que empleamos como punto de partida será un número al azar entre 1 y k.
El riesgo este tipo de muestreo está en los casos en que se dan periodicidades en la población ya que al elegir a los miembros de la muestra con una periodicidad constante (k) podemos introducir una homogeneidad que no se da en la población. Imaginemos que estamos seleccionando una muestra sobre listas de 10 individuos en los que los 5 primeros son varones y los 5 últimos mujeres, si empleamos un muestreo aleatorio sistemático con k=10 siempre seleccionaríamos o sólo hombres o sólo mujeres, no podría haber una representación de los dos sexos.
Muestreo aleatorio estratificado:
Trata de obviar las dificultades que presentan los anteriores ya que simplifican los procesos y suelen reducir el error muestral para un tamaño dado de la muestra. Consiste en considerar categorías típicas diferentes entre sí (estratos) que poseen gran homogeneidad respecto a alguna característica (se puede estratificar, por ejemplo, según la profesión, el municipio de residencia, el sexo, el estado civil, etc.). Lo que se pretende con este tipo de muestreo es asegurarse de que todos los estratos de interés estarán representados adecuadamente en la muestra. Cada estrato funciona independientemente, pudiendo aplicarse dentro de ellos el muestreo aleatorio simple o el estratificado para elegir los elementos concretos que formarán parte de la muestra. En ocasiones las dificultades que plantean son demasiado grandes, pues exige un conocimiento detallado de la población. (Tamaño geográfico, sexos, edades,...).
La distribución de la muestra en función de los diferentes estratos se denomina afijación, y puede ser de diferentes tipos:
Afijación Simple: A cada estrato le corresponde igual número de elementos muéstrales.
Afijación Proporcional: La distribución se hace de acuerdo con el peso (tamaño) de la población en cada estrato.
Afijación Optima: Se tiene en cuenta la previsible dispersión de los resultados, de modo que se considera la proporción y la desviación típica. Tiene poca aplicación ya que no se suele conocer la desviación.
- 3 -
Muestreo aleatorio por conglomerados:
Los métodos presentados hasta ahora están pensados para seleccionar directamente los elementos de la población, es decir, que las unidades muéstrales son los elementos de la población.
En el muestreo por conglomerados la unidad muestral es un grupo de elementos de la población que forman una unidad, a la que llamamos conglomerado. Las unidades hospitalarias, los departamentos universitarios, una caja de determinado producto, etc., son conglomerados naturales. En otras ocasiones se pueden utilizar conglomerados no naturales como, por ejemplo, las urnas electorales. Cuando los conglomerados son áreas geográficas suele hablarse de "muestreo por áreas".
El muestreo por conglomerados consiste en seleccionar aleatoriamente un cierto numero de conglomerados (el necesario para alcanzar el tamaño muestral establecido) y en investigar después todos los elementos pertenecientes a los conglomerados elegidos.
- 4 -
Métodos de muestreo no probabilísticos
A veces, para estudios exploratorios, el muestreo probabilístico resulta excesivamente costoso y se acude a métodos no probabilísticos, aun siendo conscientes de que no sirven para realizar generalizaciones, pues no se tiene certeza de que la muestra extraída sea representativa, ya que no todos los sujetos de la población tienen la misma probabilidad de se elegidos. En general se seleccionan a los sujetos siguiendo determinados criterios procurando que la muestra sea representativa.
de Conveniencia
· de Juicios
por Cuotas
de Bola de Nieve
Discrecional
Muestreo por cuotas:
También denominado en ocasiones "accidental". Se asienta generalmente sobre la base de un buen conocimiento de los estratos de la población y/o de los individuos más "representativos" o "adecuados" para los fines de la investigación. Mantiene, por tanto, semejanzas con el muestreo aleatorio estratificado, pero no tiene el carácter de aleatoriedad de aquél.
En este tipo de muestreo se fijan unas "cuotas" que consisten en un número de individuos que reúnen unas determinadas condiciones, por ejemplo: 20 individuos de 25 a 40 años, de sexo femenino y residentes en Gijón. Una vez determinada la cuota se eligen los primeros que se encuentren que cumplan esas características. Este método se utiliza mucho en las encuestas de opinión.
Muestreo opinático o intencional:
Este tipo de muestreo se caracteriza por un esfuerzo deliberado de obtener muestras "representativas" mediante la inclusión en la muestra de grupos supuestamente típicos. Es muy frecuente su utilización en sondeos preelectorales de zonas que en anteriores votaciones han marcado tendencias de voto.
Muestreo casual o incidental:
Se trata de un proceso en el que el investigador selecciona directa e intencionadamente los individuos de la población. El caso más frecuente de este procedimiento el utilizar como muestra los individuos a los que se tiene fácil acceso (los profesores de universidad emplean con mucha frecuencia a sus propios alumnos).
Bola de nieve:
Se localiza a algunos individuos, los cuales conducen a otros, y estos a otros, y así hasta conseguir una muestra suficiente. Este tipo se emplea muy frecuentemente cuando se hacen estudios con poblaciones "marginales", delincuentes, sectas, determinados tipos de enfermos, etc.
- 5 -
Muestreo Discrecional · A criterio del investigador los elementos son elegidos sobre lo que él cree que pueden aportar al estudio. · Ej. : muestreo por juicios; cajeros de un banco o un supermercado; etc.
Ventajas e inconvenientes de los distintos tipos de muestreo probabilístico
CARACTERISTICAS
VENTAJAS
INCONVENIENTES
Aleatorio simple
Se selecciona una muestra de tamaño n de una población de N unidades, cada elemento tiene una probabilidad de inclusión igual y conocida de n/N.
Sencillo y de fácil comprensión.
Cálculo rápido de medias y varianzas.
Se basa en la teoría estadística, y por tanto existen paquetes informáticos para analizar los datos
Requiere que se posea de antemano un listado completo de toda la población. Cuando se trabaja con muestras pequeñas es posible que no represente a la población adecuadamente.
Sistemático
Conseguir un listado de los N elementos de la población
Determinar tamaño muestral n.
Definir un intervalo k= N/n.
Elegir un número aleatorio, r, entre 1 y k (r= arranque aleatorio).
Seleccionar los elementos de la lista.
Fácil de aplicar.
No siempre es necesario tener un listado de toda la población.
Cuando la población está ordenada siguiendo una tendencia conocida, asegura una cobertura de unidades de todos los tipos.
Si la constante de muestreo está asociada con el fenómeno de interés, las estimaciones obtenidas a partir de la muestra pueden contener sesgo de selección
Estratificado
En ciertas ocasiones resultará conveniente estratificar la muestra según ciertas variables de interés. Para ello debemos conocer la composición estratificada de la población objetivo a hacer un muestreo. Una vez calculado el tamaño muestral apropiado, este se reparte de manera proporcional entre los distintos estratos definidos en la población usando una simple regla de tres.
Tiende a asegurar que la muestra represente adecuadamente a la población en función de unas variables seleccionadas.
Se obtienen estimaciones más precisa
Su objetivo es conseguir una muestra lo más semejante posible a la población en lo que a la o las variables estratificadoras se refiere.
Se ha de conocer la distribución en la población de las variables utilizadas para la estratificación.
Conglomerados
Se realizan varias fases de muestreo sucesivas (polietápico)
La necesidad de listados de las unidades de una etapa se limita a aquellas unidades de muestreo seleccionadas en la etapa anterior.
Es muy eficiente cuando la población es muy grande y dispersa.
No es preciso tener un listado de toda la población, sólo de las unidades primarias de muestreo.
El error estándar es mayor que en el muestreo aleatorio simple o estratificado.
El cálculo del error estándar es complejo.
TABLAS

Luego que producto de la observación estadísticase captaron los datos y atributos del fenómeno-objeto de estudio, se hace necesario proceder a tabular esta información con el objetivo de conocer estadísticamente el fenómeno. A este proceso de tabulación de la información se la llama distribución de frecuencias, y lo definiremos como un método para organizar y resumir datos en una tabla estadística. Para una mejor comprensión del tema es necesario adoptar las siguientes concepciones teóricas:
Es obvio que todo estudio estadístico ha de estar referido a un conjunto o colección de personas o cosas. Este conjunto de personas o casas es lo que denominaremos población. Que se entiende como un conjunto de medidas cuando éstas provienen de una característica cuantitativa, o como el recuento de todas las unidades que presentan una característica común, siendo esta cualitativa. También se puede definir a la población como un conjunto de elementos o unidades.
Las personas o cosas que forman parte de la población se denominan elementos. En sentido estadístico un elemento puede ser algo con existencia real (tangible y observable), como un automóvil o una casa, o algo más abstracto como la temperatura, un voto, o un intervalo de tiempo.
A su vez cada elemento de la población tiene una serie de característica que puede ser objeto del estudio estadístico. Así por ejemplo, si consideramos como elemento a una persona, podemos distinguir en ella los siguientes caracteres: sexo, edad, nivel de estudios, profesión, peso, altura, color de cabellos, etc. Luego por tanto de cada elemento de la población podremos estudiar uno o más aspectos cualidades o caracteres.
La población puede ser según su tamaño de dos tipos:
población finita: cuando el número de elementos es finito, por ejemplo el número de estudiantes de la Universidad de Panamá, o de una facultad o especialidad.
Población infinita: cuando el número de elementos es infinito, o tan grande que pudiese considerarse infinitos. Como por ejemplo si se realizase un estudio sobre los productos disponibles en el mercado, hay tantos y de tantas cualidades y precios que esta población podría considerarse infinita.
MEDIDAS DE DISPERCION O VARIABILIDAD
d=X-media y N = al número total de los datos.
hallar la desviacion media de la serie: 3, 8, 5, 9 y 10
ejemplo de las disperciones o variaciones de la media.
Está relacionada con la desviación estándar o desviación típica, que se suele denotar por la letra griega σ (sigma) y que es la raíz cuadrada de la varianza,
lunes, 23 de marzo de 2009
TABLA DE DOBLE ENTRADA

Tablas de doble entrada: También llamadas tablas de contingencias, son aquellas tablas de datos referentes a dos variables, formada, en las cabeceras de las filas, por las categorías o valores de una variable y en las de las columnas por los de la otra, y en las casillas de la tabla, por las frecuencias o numero de elementos que reúnen a la vez las dos categorías o valores de las dos variables que se cruzan en cada casilla. Para la tabulación de un material agrupado de observaciones simultaneas de dos variables aleatorias necesitaremos una tabla descrita como anteriormente lo describimos, las reglas para agrupar son las mismas que en el caso de una sola variable.
Este tipo de tablas brindan información estadística de dos eventos relacionados entre sí, es útil en casos en los cuales los experimentos son dependientes de otro experimento, mas adelante aparecen mas aplicaciones del análisis estadístico bivariable.
Descripción
En una tabla de doble entrada, los datos se muestran en columnas y filas al igual que en las tablas. Sin embargo, en comparación con las tablas, cada columna tiene por lo menos un encabezado y cada fila tiene por lo menos un encabezado de fila. Los datos correspondientes aparecen en la intersección de los encabezados de la columna y la fila: esta sección corresponde al "cuerpo".
El ejemplo: de la tabla de doble entrada muestra el volumen de negocios por prestación y por trimestre. Los rótulos de las prestaciones son encabezados de fila y, los rótulos de trimestre son encabezados de columna. El volumen de negocios para cada prestación para cada trimestre aparece en el cuerpo.
Para entender la disposición de los elementos en una tabla de doble entrada, imagínese la tabla de doble entrada como un bloque terminado. Los objetos que se colocan en el cuadrante inferior izquierdo de la tabla de doble entrada proporcionan los datos para los encabezados de fila; los objetos colocados en el cuadrante superior derecho proporcionan los datos para los encabezados de columna, y los objetos del cuadrante inferior derecho proporcionan los datos para el cuerpo de la tabla. No puede colocar ningún objeto en el cuadrante superior izquierdo.
Uso :
Presentación de la información en un formato multidimensional de filas y columnas, donde cada elemento está asociado a otro. Por ejemplo, un tipo de prestación podría estar asociado a un centro de vacaciones en particular.
Importante :
Organice los objetos en el orden en que desea que aparezcan en el bloque.
Depende de si el documento contiene secciones o no, la disposición del cuerpo de la tabla de doble entrada corresponde siempre a la organización de los objetos del panel Bloque.
Los objetos de tipo indicador no se pueden utilizar en los encabezados verticales u horizontales; sólo se pueden utilizar en el cuerpo de la tabla de doble entrada.
Puede utilizar más de un objeto en el cuerpo de la tabla de doble entrada.
Puede utilizar varios objetos en los encabezados verticales u horizontales. Por ejemplo, podría utilizar los objetos Tipos de prestaciones y Prestaciones en un encabezado, de modo que tanto el tipo de prestaciones como las prestaciones se muestren en la tabla de doble entrada.
Los objetos no tienen que formar parte de la misma clase. Por ejemplo, podría utilizar los objetos Tipo de prestaciones y Centro de vacaciones para mostrar información por tipo de prestaciones por centro de vacaciones.
Lo más importante asi nos damos cuenta que la tabla de doble estrada se utizara si se esta estudiando 2 fenomenos como nos ejemplificaban en el aula peso y edad .
MEDIDAS DE FORMA

El día 9 de marzo nos ampliaron el tema de MEDIDAS DE FORMA las cuales forman el gremio estadistico en las medidas de forma encontramos "EL SESGO" Y "LA CURTOSIS".
EL SESGO:Mide las desviaciones de las MTC., Ya que el seesgo es el grado de asimetría o falta de asimetría, de una distribucion, si el poligono de frecuencias visualizado de una distribucion tiene una cola más larga a la derecha del máximo central que a la izquierda, se dice que la distribucion esta sesgada a la derecha o que tiene sesgo positivo(asimetría positiva) y si al contrario se dice que tiene sesgo (asimetría negativa) en la asimetria encontramos si es:
a)asimetricamente + = cuado el sg es mayor a 0
b)normal= cuado el sg = 0
c)simetricamente - cuando el sg es menor a 0
formula:
_
Sg= __X -Md__ = Sesgo es igual a: media menos la moda partido o dividido desviacion.
S
los datos más utilizados son los sig:
moda , media, desviación.
& pero si existen dos o más modas se utilizara otra formula:
Sg=_x-Md__= sesgo es igual a: media menos la mediana partido o dividido desviación
si la asimetria es NORMAL se aplicara la curtosis : si y solo si la asimertría es normal.
CURTOSIS:Es la agudeza de la curva normal , esta agudeza puede ser alta , baja, o intermedia dando lugar a diferentes tipos de curvas como: plato, meso, leptocúrtica,

k<0.263>
k=0.263 = mesocutica.
k>0.263 = leptocurtica.
la fórmula a utilizar el la siguiente:
1/2 (Q3-Q1)
K= __________
P90-P10
curtosis igual a un medio entre cuartil 3 menos cualtil 1 dividido percentil de 90 menos percentil de 10
las medidas de forma son complejas´pero la cual nos facilitan a detectar las asimetrias del fenomeno estudiado...
sábado, 14 de marzo de 2009
MEDIDAS DE POSICION
Al describir grupos de observaciones, con frecuencia se desea describir el grupo con un solo número. Para tal fin, desde luego, no se usará el valor más elevado ni el valor más pequeño como único representante, ya que solo representan los extremos más bien que valores típicos. Entonces sería más adecuado buscar un valor central. Las medidas que describen un valor típico en un grupo de observaciones suelen llamarse medidas de tendencia central. Es importante tener en cuenta que estas medidas se aplican a grupos más bien que a individuos. Un promedio es una característica de grupo, no individual.
Entre las medidas de tendencia central tenemos:
CUARTILES(Qk9)
DECILES:(Dk)
CENTILES O PERCENTILES:(Ck)
QUINTILES: (Kk)
Cartiles:
Cuartiles. Son los puntos que dividen a una distribución de valores en cuatro porciones iguales o intervalos. Se representan por , , y se ilustran en el esquema siguiente:
Q1=25%, Q2=50% Q3=75% Q4=100% =1,2,3,4
Ordenamos los datos de menor a mayor.
2 Buscamos el lugar que ocupa cada cuartil mediante la expresión .
Lo cuartiles son representados como . El primer cuartil considera el 25% de la información a su izquierda y el 75% a la derecha; para el segundo cuartil considera el 50% de la información tanto a la derecha como a la izquierda, este coincide con la mediana; el tercer cuartil considera el 75% de la información a la izquierda y el 75% a la derecha. El cuarto cuartil, que no fue indicado en el gráfico considera a toda la información. Por lo anterior podemos afirmar que los cuartiles son tres valores que dividen a la serie de datos en cuatro partes iguales, como se puede apreciar el gráfico.
El cálculo para los cuartiles se determina a través de la siguiente expresión:
donde :
k
Orden del cuartil
Li=Límite inferior del intervalo que contiene al cuartil
Fa=Frecuencia acumulada considerada al intervalo donde se encuentra
Frecuencia del intervalo que contiene el cuartil
n=Número de mediciones
i=Amplitud del intervalo
DECILES:
Los deciles son los nueve valores que dividen la serie de datos en diez partes iguales.
Los deciles dan los valores correspondientes al 10%, al 20%... y al 90% de los datos.
D5 coincide con la mediana.
Cálculo de los deciles
En primer lugar buscamos la clase donde se encuentra , en la tabla de las frecuencias acumuladas.
Cálculo del primer decil
Cálculo del segundo decil
Cálculo del tercer decil
Cálculo del cuarto decil
Cálculo del quinto decil
Cálculo del sexto decil
Cálculo del séptimo decil
Cálculo del octavo decil
Cálculo del noveno decil
Quintiles:
Artículo principal:
Se representan con la letra K.
Es el primer quintil. Separa a la muestra dejando el 20% de los datos a su izquierda.
Es el segundo quintil. Es el valor que indica que el 40% de los datos son menores.
Es el tercer quintil. Indica que el 60% de los datos son menores que él.
Es el cuarto quintil. Separa al 80% de los datos del otro 20%.
Percentiles O Centiles:
Se representan con la letra C.
Es el percentil i-ésimo, donde la i toma valores del 1 al 99. El i % de la muestra son valores menores que él y el 100-i % restante son mayores.
Cuando los datos no están agrupados en intervalos, los cuartiles, así como el resto de las medidas de posición, tienen un valor claro. Sin embargo, cuando tenemos una agrupación de los datos ya no es tan sencillo realizar el cálculo. Sí que resulta claro ver en cuál de los intervalos está el cuartil (quintil, decil o percentil) buscado, pero para calcular su valor exacto necesitaremos usar una fórmula.
MEDIDAS DE TENDENCIA CENTRAL
MEDIA, MEDIANA, NODA, NEDIA ARNONICA, MEDIA GEOMETRICA, MEDIA CUADRATICA.
La media aritmética o promedio, de una cantidad finita de números, es igual a la suma de todos ellos dividida entre el número de sumandos. Es uno de los principales estadísticos muestrales.
Expresada de forma más intuitiva, podemos decir que la media (aritmética) es la cantidad total de la variable distribuida a partes iguales entre cada observación. Por ejemplo, si en una habitación hay tres personas, la media de dinero que tienen en sus bolsillos sería el resultado de tomar todo el dinero de los tres y dividirlo a partes iguales entre cada uno de ellos. Es decir, la media es una forma de resumir la información de una distribución (dinero en el bolsillo) suponiendo que cada observación (persona) tendría la misma cantidad de la variable.
También la media aritmética puede ser denominada como centro de gravedad de una distribución, el cual no es necesariamente la mitad.
Definición:
Dados los n números a1,a2, ... , an, la media aritmética se define simplemente como:
Por ejemplo, la media aritmética de 8, 5 y -1 es igual a:
La X, con una barra horizontal sobre el símbolo para medias de una muestra (), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
Propiedades:
La media aritmética de un conjunto de números positivos siempre es igual o superior a media geométrica:
Mediana:
En Estadística una mediana es el valor de la variable que deja el mismo número de datos antes y después que él, una vez ordenados estos. De acuerdo con esta definición el conjunto de datos menores o iguales que la mediana representarán el 50% de los datos, y los que sean mayores que la mediana representarán el otro 50% del total de datos de la muestra. La mediana coincide con el percentil 50, con el segundo cuartil y con el quinto decil.
Cálculo:
Existen dos estrategias para calcular la mediana: Considerando los datos tal cual, sin agruparlos, o bien cuando los tenemos agrupados en intervalos de clase. Veamos cada una de ellas.
Datos sin agrupar :
Considerando los datos de una muestra ordenada en orden creciente y designando la mediana como Me, distinguimos dos casos:
a) Si n es impar, la mediana es el valor que ocupa la posición una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central. Es decir: .
Por ejemplo, si tenemos 5 datos, que ordenados son: x1 = 3, x2 = 6, x3 = 7, x4 = 8, x5 = 9 => El valor central es el tercero: . Este valor deja dos datos por debajo (x1, x2) y otros dos por encima de él (x4, x5).
b) Si n es par, la mediana es la media aritmética de las dos observaciones centrales. Cuando n es par, los dos datos que están en el centro de la muestra ocupan las posiciones y . Es decir: .
Por ejemplo, si tenemos 6 datos, que ordenados son: x1 = 3, x2 = 6, x3 = 7, x4 = 8, x5 = 9, x6 = 10 => Hay dos valores que están por debajo del y otros dos que quedan por encima del siguiente dato . Por tanto, cabe considerar la mediana como la media aritmética de estos dos datos: .
Datos agrupados
Al tratar con datos agrupados, si n/2 coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abcisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas, utilizando la siguiente equivalencia
Moda:
Es el valor que cuenta con una mayor frecuencia en una distribución de datos.
Hablaremos de una distribución bimodal de los datos, cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima. Una distribución trimodal de los datos es en la que encontramos tres modas. Si todas las variables tienen la misma frecuencia diremos que no hay moda.
El intervalo modal es el de mayor frecuencia absoluta. Cuando tratamos con datos agrupados antes de definir la moda, se ha de definir el intervalo modal.
La moda, cuando los datos están agrupados, es un punto que divide al intervalo modal en dos partes de la forma p y c-p, siendo c la amplitud del intervalo, que verifiquen que:
Siendo la frecuencia absoluta del intervalo modal las frecuencias absolutas de los intervalos anterior y posterior, respectivamente, al intervalo modal.
Media armónica:
La media armónica , representada H, de una cantidad finita de números es igual al recíproco, o inverso, de la media aritmética de los recíprocos de dichos números
Así, dados los números a1,a2, ... , an, la media armónica será igual a:
La media armónica resulta poco influida por la existencia de determinados valores mucho más grandes que el conjunto de los otros, siendo en cambio sensible a valores mucho más pequeños que el conjunto.
La media armónica no está definida en el caso de la existencia en el conjunto de valores nulos.
@Desviación estándar:
La desviación estándar (o desviación típica) es una medida de dispersión para variables de razón (ratio o cociente) y de intervalo, de gran utilidad en la estadística descriptiva. Es una medida (cuadrática) que informa de la media de distancias que tienen los datos respecto de su media aritmética, expresada en las mismas unidades que la variable.
Para abordar las cuestiones que comentábamos en el párrafo anterior, nos valemos de herramientas como la varianza y la desviación estándar. Ambas medidas están estrechamente relacionadas ya que definimos una a partir de la otra.
Para conocer con detalle un conjunto de datos, no basta con conocer las medidas de tendencia central, sino que necesitamos conocer también la desviación que representan los datos en su distribución respecto de la media aritmética de dicha distribución, con objeto de tener una visión de los mismos más acorde con la realidad a la hora de describirlos e interpretarlos para la toma de decisiones.
@La varianza representa la media aritmética de las desviaciones con respecto a la media elevadas al cuadrado. Si atendemos a la colección completa de datos (la población en su totalidad) obtenemos la varianza poblacional; y si por el contrario prestamos atención sólo a una muestra de la población, obtenemos en su lugar la varianza muestral. Las expresiones de estas medidas son las que aparecen a continuación.
Expresión de la varianza muestral:
Expresión de la varianza poblacional:
Expresión de la desviación estándar poblacional:
El término desviación estándar fue incorporado a la estadística por Karl Pearson en 1894.
Por la formulación de la varianza podemos pasar a obtener la desviación estándar, tomando la raíz cuadrada positiva de la varianza. Así, si efectuamos la raíz de la varianza muestral, obtenemos la desviación típica muestral; y si por el contrario, efectuamos la raíz sobre la varianza poblacional, obtendremos la desviación típica poblacional.
Desviaciones estándar en una distribución normal
Expresión de la desviación estándar muestral:
También puede ser tomada como (FORMULA).
Media cuadrática:Es igual a la raíz cuadrada de la suma de los cuadrados de los valores dividida entre el número de datos:
A veces la variable toma valores positivos y negativos, como ocurre, por ejemplo, en los errores de medida. En tal caso se puede estar interesado en obtener un promedio que no recoja los efectos del signo. Este problema se resuelve, mediante la denominada media cuadrática. Consiste en elevar al cuadrado todas las observaciones (así los signos negativos desaparecen), en obtener después su media aritmética y en extraer, finalmente, la raíz cuadrada de dicha media para volver a la unidad de medida original.
Media geométrica:
De una cantidad finita de números (digamos 'n' números) es la raíz n-ésima del producto de todos los números.
Por ejemplo, la media geométrica de 2 y 18 es
Otro ejemplo, la media de 1, 3 y 9 seria
Sólo es relevante la media geométrica si todos los números son positivos. Si uno de ellos es 0, entonces el resultado es 0. Si hay un número negativo (o una cantidad impar de ellos) entonces la media geométrica es, o bien negativa o bien inexistente en los números reales.
En muchas ocasiones se utiliza su trasformación en el manejo estadístico de variables con distribución no normal.
La media geométrica es relevante cuando varias cantidades son multiplicadas para producir un total.
las mediadas de tendencia central son necesaria e importartantes en el ambito estadistico:
Número artificial creado para representar un conjunto de números.
La media aritmética, o promedio (llamada media) de a1, a2, a3, . . ., an está dada por:
(a1+a2+a3+. . .+an)/n
Si el conjunto de números a1, a2, a3, . . ., an ocurre con las frecuencias f1, f2, f3, . . ., fn, entonces la media aritmética está dada por:
(f1a1+f2a2+f3a3+ ... +fnan)/(f1+f2+f3+ ... +fn)
La media geométrica de a1, a2, a3, . . ., an está dada por:
(a1×a2×a3×...×a3)1/n
sera necesario ulilizar formulas las cuales sera obtenida los resultados decesados.
jueves, 12 de marzo de 2009
MEDIDAS DE TENDENCIA CENTRAL
Saltar a navegación, búsqueda
Para otros usos de este término, véase mediana
En Estadística, una mediana es el valor de la variable que deja el mismo número de datos antes y después que él, una vez ordenados estos. De acuerdo con esta definición el conjunto de datos menores o iguales que la mediana representarán el 50% de los datos, y los que sean mayores que la mediana representarán el otro 50% del total de datos de la muestra. La mediana coincide con el percentil 50, con el segundo cuartil y con el quinto decil.
Contenido1 Cálculo
1.1 Datos sin agrupar
1.2 Datos agrupados
2 Ejemplos
2.1 Ejemplo ( "N" impar )
2.2 Ejemplo ( "N" par )
2.2.1 Ejemplo
2.2.1.1 Ahora mostramos el calculo de forma general:
2.2.1.1.1 Consideramos:
2.3 Método proyectivo
3 Véase también
Cálculo
Existen dos estrategias para calcular la mediana: Considerando los datos tal cual, sin agruparlos, o bien cuando los tenemos agrupados en intervalos de clase. Veamos cada una de ellas.
Datos sin agrupar
Considerando los datos de una muestra ordenada en orden creciente y designando la mediana como Me, distinguimos dos casos:
a) Si n es impar, la mediana es el valor que ocupa la posición una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central. Es decir: .
Por ejemplo, si tenemos 5 datos, que ordenados son: x1 = 3, x2 = 6, x3 = 7, x4 = 8, x5 = 9 => El valor central es el tercero: . Este valor deja dos datos por debajo (x1, x2) y otros dos por encima de él (x4, x5).
b) Si n es par, la mediana es la media aritmética de las dos observaciones centrales. Cuando n es par, los dos datos que están en el centro de la muestra ocupan las posiciones y . Es decir: .
Por ejemplo, si tenemos 6 datos, que ordenados son: x1 = 3, x2 = 6, x3 = 7, x4 = 8, x5 = 9, x6 = 10 => Hay dos valores que están por debajo del y otros dos que quedan por encima del siguiente dato . Por tanto, cabe considerar la mediana como la media aritmética de estos dos datos: .
Datos agrupados
Al tratar con datos agrupados, si n/2 coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abcisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas, utilizando la siguiente equivalencia:
Dónde Ni y Ni-1 son las frecuencias absolutas tales que Ni-1< n/2
Se ha sugerido que este artículo o sección sea fusionado con Promedio (ver la discusión al respecto).Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales en WP:TAB/F.
La media aritmética o promedio, de una cantidad finita de números, es igual a la suma de todos ellos dividida entre el número de sumandos. Es uno de los principales estadísticos muestrales
Expresada de forma más intuitiva, podemos decir que la media (aritmética) es la cantidad total de la variable distribuida a partes iguales entre cada observación. Por ejemplo, si en una habitación hay tres personas, la media de dinero que tienen en sus bolsillos sería el resultado de tomar todo el dinero de los tres y dividirlo a partes iguales entre cada uno de ellos. Es decir, la media es una forma de resumir la información de una distribución (dinero en el bolsillo) suponiendo que cada observación (persona) tendría la misma cantidad de la variable.
También la media aritmética puede ser denominada como centro de gravedad de una distribución, el cual no es necesariamente la mitad.
Definición:
Dados los n números a1,a2, ... , an, la media aritmética se define simplemente como:
Por ejemplo, la media aritmética de 8, 5 y -1 es igual a:
La X, con una barra horizontal sobre el símbolo para medias de una muestra (), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
Otras medias estadísticas
Es el dato que más se repite en la cuenta. Si existen dos datos que se repite un número igual de veces entonces el conjunto será bimodal. Ejemplo:
Número de personas en distintos carros en una carretera :5-7-4-6-9-5-6-1-5-3-7
En estadística la moda es el valor que cuenta con una mayor frecuencia en una distribución de datos.
Hablaremos de una distribución bimodal de los datos, cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima.
Cuando en una distribución de datos se encuentran tres o más modas, entonces es multimodal.Si todas las variables tienen la misma frecuencia diremos que no hay moda.
Cuando tratamos con datos agrupados antes de definir la moda, se ha de definir el intervalo modal. El intervalo modal es el de mayor frecuencia absoluta.
La moda, cuando los datos están agrupados, es un punto que divide al intervalo modal en dos partes de la forma p y c-p, siendo c la amplitud del intervalo, que verifiquen que:
Siendo ni la frecuencia absoluta del intervalo modal y ni − 1 y ni + 1 las frecuencias absolutas de los intervalos anterior y posterior, respectivamente, al Las calificaciones en la asignatura de Matemáticas de 39 alumnos de una clase viene dada por la siguiente tabla (debajo):
Calificaciones
1
2
3
4
5
6
7
8
9
Número de alumnos
2
2
4
5
8
9
3
4
2
La media armónica , representada H, de una cantidad finita de números es igual al recíproco, o inverso, de la media aritmética de los recíprocos de dichos números
Así, dados los números a1,a2, ... , an, la media armónica será igual a:
La media armónica resulta poco influida por la existencia de determinados valores mucho más grandes que el conjunto de los otros, siendo en cambio sensible a valores mucho más pequeños que el conjunto.
La media armónica no está definida en el caso de la existencia en el conjunto de valores nulos.
MEDIA CUADRATICA:
Esta media como medida de asociación tiene aplicaciones tanto en ciencias biológicas como en medicina.
A veces la variable toma valores positivos y negativos, como ocurre, por ejemplo, en los errores de medida. En tal caso se puede estar interesado en obtener un promedio que no recoja los efectos del signo. Este problema se resuelve, mediante la denominada media cuadrática. Consiste en elevar al cuadrado todas las observaciones (así los signos negativos desaparecen), en obtener después su media aritmética y en extraer, finalmente, la raíz cuadrada de dicha media para volver a la unidad de medida original.
Otras medias estadísticaS son la media aritmética, la media ponderada, media cuadrática, media generalizad , media armónica y la media aritmética geométrica
La media geométrica de una cantidad finita de números (digamos 'n' números) es la raíz n-ésima del producto de todos los números.
Por ejemplo, la media geométrica de 2 y 18 es
Otro ejemplo, la media de 1, 3 y 9 seria
Sólo es relevante la media geométrica si todos los números son positivos. Si uno de ellos es 0, entonces el resultado es 0. Si hay un número negativo (o una cantidad impar de ellos) entonces la media geométrica es, o bien negativa o bien inexistente en los números reales.
En muchas ocasiones se utiliza su trasformación en el manejo estadístico de variables con distribución no normal.
La media geométrica es relevante cuando varias cantidades son multiplicadas para producir un total.
Un diagrama donde cada valor de datos es dividido en una "hoja" (normalmente el último dígito) y un "tallo" (los otros dígitos). Por ejemplo "32" sería dividido en "3" (tallo) y "2" (hoja).Los valores del "tallo" se escriben hacia abajo y los valores "hoja" van a la derecha (o izquierda) del los valores tallo.El "tallo" es usado para agrupar los puntajes y cada "hoja" indica los puntajes individuales dentro de cada grupo.