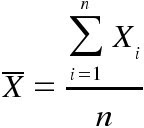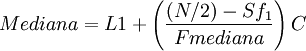PERMUTACIONES:
PERMUTACIONES:Es todo arreglo de elementos en donde nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.
Para ver de una manera objetiva la diferencia entre una combinación y una permutación, plantearemos cierta situación.
Suponga que un salón de clase está constituido por 35 alumnos. a) El maestro desea que tres de los alumnos lo ayuden en actividades tales como mantener el aula limpia o entregar material a los alumnos cuando así sea necesario.
b) El maestro desea que se nombre a los representantes del salón (Presidente, Secretario y Tesorero).
Solución:
a) Suponga que por unanimidad se ha elegido a Daniel, Arturo y a Rafael para limpiar el aula o entregar material, (aunque pudieron haberse seleccionado a Rafael, Daniel y a Enrique, o pudo haberse formado cualquier grupo de tres personas para realizar las actividades mencionadas anteriormente).
¿Es importante el orden como se selecciona a los elementos que forma el grupo de tres personas?
Reflexionando al respecto nos damos cuenta de que el orden en este caso no tiene importancia, ya que lo único que nos interesaría es el contenido de cada grupo, dicho de otra forma, ¿quiénes están en el grupo? Por tanto, este ejemplo es una combinación, quiere decir esto que las combinaciones nos permiten formar grupos o muestras de elementos en donde lo único que nos interesa es el contenido de los mismos.
b) Suponga que se han nombrado como representantes del salón a Daniel como Presidente, a Arturo como secretario y a Rafael como tesorero, pero resulta que a alguien se le ocurre hacer algunos cambios, los que se muestran a continuación:
CAMBIOS PRESIDENTE:
Daniel
Arturo
Rafael
Daniel
SECRETARIO:
Arturo
Daniel
Daniel
Rafael
TESORERO:
Rafael
Rafael
Arturo
Arturo
Ahora tenemos cuatro arreglos, ¿se trata de la misma representación?
Creo que la respuesta sería no, ya que el cambio de función que se hace a los integrantes de la representación original hace que definitivamente cada una de las representaciones trabaje de manera diferente, ¿importa el orden de los elementos en los arreglos?. La respuesta definitivamente sería sí, luego entonces las representaciones antes definidas son diferentes ya que el orden o la forma en que se asignan las funciones sí importa, por lo tanto es este caso estamos tratando con permutaciones.
A continuación obtendremos las fórmulas de permutaciones y de combinaciones, pero antes hay que definir lo que es n! (ene factorial), ya q
ue está involucrado en las fórmulas que se obtendrán y usarán para la resolución de problemas.
n!= al producto desde la unidad hasta el valo
n!= al producto desde la unidad hasta el valo
que ostenta n.
n!= 1 x 2 x 3 x 4 x………..x n
Ejem.
10!=1 x 2 x 3 x 4 x………x 10=3,628,800
8!= 1 x 2 x 3 x 4 x………x 8=40,320
6!=1 x 2 x 3 x 4 x……….x 6=720, etc., etc.
1).Obtención de fórmula de permutaciones.
Para hacer esto, partiremos de un ejemplo.
¿Cuántas maneras hay de asignar los cuatro primeros lugares de un concurso de creatividad que se verifica en las instalaciones de nuestro instituto, si hay 14 participantes?
n!= 1 x 2 x 3 x 4 x………..x n
Ejem.
10!=1 x 2 x 3 x 4 x………x 10=3,628,800
8!= 1 x 2 x 3 x 4 x………x 8=40,320
6!=1 x 2 x 3 x 4 x……….x 6=720, etc., etc.
1).Obtención de fórmula de permutaciones.
Para hacer esto, partiremos de un ejemplo.
¿Cuántas maneras hay de asignar los cuatro primeros lugares de un concurso de creatividad que se verifica en las instalaciones de nuestro instituto, si hay 14 participantes?
Solución:
Haciendo uso del principio multiplicativo,
14×13×12×11 = 24,024 maneras de asignar los primeros tres lugares del concurso
Esta solución se debe, a que al momento de asignar el primer lugar tenemos a 14 posibles candidatos, una vez asignado ese lugar nos quedan 13 posibles candidatos para el segundo lugar, luego tendríamos 12 candidatos posibles para el tercer lugar y por último tendríamos 11 candidatos posibles para el cuarto lugar.
Luego si n es el total de participantes en el concurso y r es el número de participantes que van a ser premiados, y partiendo de la expresión anterior, entonces.
14×13×12×11= n x (n - 1) x (n - 2) x ………. x (n – r + 1)
si la expresión anterior es multiplicada por (n – r)! / (n – r)!, entonces
= n x (n –1 ) x (n – 2) x ……… x (n – r + 1) (n – r)! / (n – r)!
= n!/ (n – r)!
Por tanto, la fórmula de permutaciones de r objetos tomados de entre n objetos es:
Esta fórmula nos permitirá obtener todos aquellos arreglos en donde el orden es importante y solo se usen parte ® de los n objetos con que se cuenta, además hay que hacer notar que no se pueden repetir objetos dentro del arreglo, esto es, los n objetos son todos diferentes.
Entonces, ¿ qué fórmula hay que usar para arreglos en donde se utilicen los n objetos con que se cuenta?
Si en la fórmula anterior se sustituye n en lugar de r, entonces.
nPn= n!/ (n –n)! = n! / 0! = n! / 1 = n!
Como 0! = 1 de acuerdo a demostración matemática, entonces
nPn= n!

COMENTARIO:
Las permutaciones son los arreglos posibles de cada problema plantado ya que para ello se debe de analizar meramente cada problema sabviendo que las posibilidades a tener tendrab que ser realizadas en un determunado orden, bien tambien una permutacion es cualquier subconjunto oedenado de un conjunto universal o sea se le llama permutación de n elementos a los diferentes grupos que pueden hacerse tomandolos todos cada vez. sin olvidar que tambien lo podemos realizar a través de la formula dada anteriormente, por lo que es necesrio e importante conocer las posibilidades.











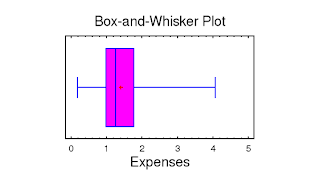


 El diagrama de disperción define entonces en la grafica se define que puede existir regresion lineal positiva, negativa o incluso nula.
El diagrama de disperción define entonces en la grafica se define que puede existir regresion lineal positiva, negativa o incluso nula.